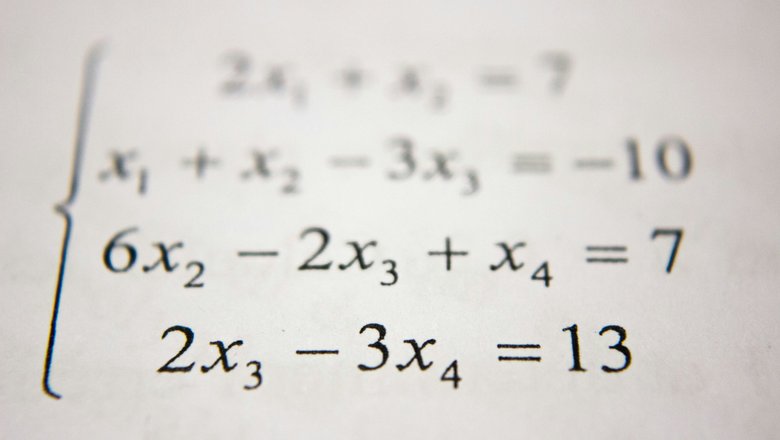
Раньше базовой арифметикой пользовались многие почти каждый день. Так, например, она нужна для того, чтобы посчитать сумму товаров в магазинном чеке, а знания в геометрии были нужны плотникам. Геодезистам и штурманам требовалась также тригонометрия. Инженерное дело было немыслимо без дифференциального и интегрального исчисления.
Однако сейчас сумму в чеке считает кассовый терминал, он же учитывает скидки и начисляет налог с продаж. Поэтому может показаться, что математика ушла в прошлое, но математик и популяризатор науки Иэн Стюарт в своей книге «Это база: Зачем нужна математика в повседневной жизни» пишет, что это мнение ошибочно. Первую главу опубликовал журнал «Нож».
Многие склонны считать, что компьютеры вытесняют математиков. Однако электронные устройства в целом освобождают человека от монотонной работы. Они дают людям время подумать, помогают выискивать закономерности и добавляют в арсенал новый мощный инструмент, позволяющий развивать математику быстрее и эффективнее.
Большинство алгоритмов, которыми обладают компьютеры, опираются на математику. Многие из них основаны на базовых математических идеях.
Так, например, в алгоритме глубокого обучения искусственного интеллекта используются давно испытанные и проверенные математические концепции, такие как матрицы и взвешенные графы.
Математика сегодня нужна во многих профессиях: для разработки многих лекарств требуется статистика, без которой невозможно обеспечить их безопасность и эффективность; спутниковая связь невозможна без понимания небесной механики; прогнозирование погоды требует решения уравнений, описывающих движение атмосферных масс, количество содержащейся в них влаги, температуру и взаимодействие всех этих факторов.
Например, в 1736 году швейцарский математик Леонард Эйлер заинтересовался головоломкой, связанной с кенигсбергскими мостами. Согласно условию, нужно пройти по семи мостам через реку Преголя, но использовать каждый только один раз.
Эйлер понял, что для того, чтобы найти ответ на загадку, требуется геометрия нового типа, которая меняла обычные представления о длинах и углах. И тогда ученый не задумывался о том, что его решение пригодится в XXI веке для поисков донорской почки.
В 1890 году Джузеппе Пеано открыл заполняющую пространство кривую — непрерывная кривая, целиком заполняющая некоторый квадрат, то есть проходящая через все его точки. И он так же, как и Эйлер, вряд ли мог подумать о том, что через сотни лет его находка пригодится для программы доставки еды Meals on Wheels.
Однако помогает не только математика прошлого. Так, методы трансплантации почки опираются на многочисленные современные расширения первоначального озарения Эйлера, к которым относятся, в частности, алгоритмы комбинаторной оптимизации, позволяющие делать наилучший выбор из огромного спектра возможностей.
Математические методы используются и в компьютерной анимации. Например, благодаря «пространству форм» (пространство бесконечной размерности, состоящее из кривых, которые считаются одной и той же кривой, если различаются только координатами) анимационные последовательности становятся более плавными.
В 1959 году американский физик Юджин Вигнер прочел в Нью-Йоркском университете лекцию под названием «Непостижимая эффективность математики в естественных науках». Ученый рассказал, что неудивительно, что математика выросла в первую очередь из физических задач. Его поражает тот факт, что эта наука эффективна в областях, не связанных с ней.
Согласно одному из предположений, Вселенная «состоит» из математики, и люди всего лишь понемногу открывают для себя этот основной ее элемент.
Ранее учитель математики развеял мифы о своем предмете.




