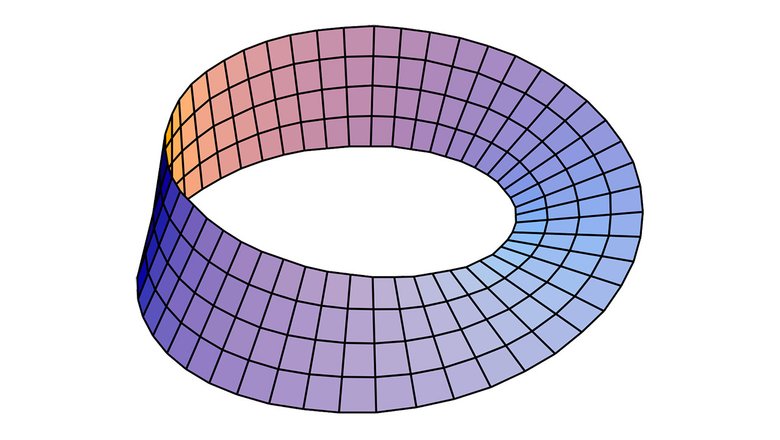
Лента Мёбиуса — занимательный математический объект. Для их создания достаточно взять полосу бумаги, сделать в ней один поворот и соединить концы. Несмотря на простоту ее формы, свойства этих фигур заставляют математиков более 150 лет искать ответы на сложные вопросы, касающиеся их структуры.
Только на протяжении последних 50 лет математики ломали голову над обманчиво простым вопросом: какова минимальная длина полосы бумаги, необходимая для создания ленты Мёбиуса без самопересечений? Этот вопрос был поставлен в 1977 году математиками Чарльзом Сидни Уивером и Бенджамином Риглером Халперном.
Ученые предположили ограничение для лент Мёбиуса: соотношение между длиной и шириной бумаги должно быть больше √3, или значением около 1,73. То есть, к примеру, полоса длиной в один сантиметр должна быть шире, чем √3 или 1,73 сантиметра. Несмотря на предположения, ученые не могли доказать свою теорию.
Ричард Шварц, математик из Университета Брауна (США), сказал, что он заинтересовался лентой Мёбиуса после того, как узнал о ней четыре года назад во время разговора с коллегой. На протяжении многих лет он предпринял несколько попыток решить эту задачу, и в 2021 году опубликовал статью с многообещающим подходом, который в конечном итоге потерпел неудачу.
Ученый не мог оставить эту проблему в покое и начал экспериментировать со сжатием бумажных лент Мёбиуса в надежде, что с наглядной двумерной формой на руках задачу будет проще решить. Но когда он разрезал одну из этих петель под углом (что было необходимо для решения его задачи оптимизации), он пришел к неожиданному результату.
Длина двухмерного листа бумаги не была похожа на параллелограмм, как он сообщал в своей первой статье. Скорее, это была трапеция — форма с четырьмя прямыми сторонами, из которых только две стороны параллельны друг другу. «Недавно я обнаружил, что допустил ошибку при постановке задачи оптимизации», — написал Шварц.
Он исправил свою ошибку и доказал предположение Уивера и Халперна. Результаты его экспериментов доступны в виде препринта arXiv.
Недавно математики узнали, сколько лотерейных билетов нужно для выигрыша. Оказалось, что это очень затратно.
Олеся Маевская





